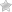Когда мы поднимаем наполненное водою ведро, то сразу чувствуем его большую тяжесть. Подняв ведро без воды, мы ощущаем только тяжесть самого сосуда. Но это ведро ведь не пустое, оно наполнено воздухом; стало быть, сам воздух не имеет никакого веса? Может быть, воздух в ведре ничего не весит потому, что уходит из открытого ведра.
Возьмем бурдюк или бычий пузырь, наполним его воздухом, завяжем и попробуем взвесить, а затем выдавим из него воздух и снова взвесим.
Окажется, что показания весов оба раза будут одинаковыми, быть, действительно, воздух ничего не весит и это можно считать доказанным? Вместе с тем, если согласиться с отсутствием веса воздуха, то многие явления покажутся непонятными.
Трубка Торричелли. Атмосферное давление на поверхность ртути в открытой чашке уравновешивает давление ртутного столба в трубке, и ртуть из нее не выливается
Почему, например, медицинские банки втягивают кожу человека. Почему, если мы наполним водой стакан с хорошо пришлифованными краями точно по эти края и накроем его бумажкой, а затем быстро перевернем стакан, то вода из стакана не выльется? Почему действует насос, перекачивающий воду снизу вверх?
Все эти явления казались долгое время необъяснимыми, но насос же и позволил открыть истину.
В поисках объяснения обратились к знаменитому ученому Галилею, тогда 80-летнему старцу. До нас дошли два варианта дальнейших событий. По первому из них Галилей будто бы смутился и не знал, что ответить. По второму варианту Галилей взвесил «пустую» бутылку, затем сильно разогрел ее, закрыл пробкой и, охладив, взвесил вторично.
Оказалось, что на этот раз бутылка весила меньше.Сохранились сведения, что в XVII веке в саду герцога Тосканско во Флоренции построили насос, чтобы перекачивать воду для фонтана на высоту больше 10 метров, но это никак не удавалось.
Насос был сделан так же хорошо, как и все другие, прекрасно работавшие, и поэтому неудача с ним казалась совершенно непонятной.
Галилей правильно объяснил уменьшение веса бутылки, указав, что при нагревании воздух расширился и был вытеснен из бутылки в атмосферу.
Следовательно, в бутылке его оказалось меньше, поэтому и вес бутылки во второй раз стал меньшим.
Таким образом Галилеи установил, что воздух имеет вес, но весит он меньше воды, и новый насос, больший, чем предшествовавшие, не работал только потому, что вес наружного воздуха не уравновешивал слишком высокого столба воды.
Несомненно, правильнее второй вариант дошедшего до нас рассказа, так как известно, что Галилей уже раньше делал подобные расчеты.
Он объяснил силу, уравновешивающую давление воздуха «силой пустоты» В те времена существовало мнение, что природа «боится пустоты», и как только где-либо пустота образуется, природа ее тотчас заполняет.
Но при этом оставалось необъяснимым то, что эта «боязнь пустоты» прекращалась выше 10 метров. Следовательно, загадка так и не была разрешена полностью.
Ученик Галилея, Торричелли продолжал исследование вопроса и произвел ряд опытов, которые позволили ему надежно доказать, что воздух имеет вес, и привели его в 1643 году к изобретению прибора, известного нам теперь под названием барометра.
Торричелли наполнил ртутью закрытую с одного конца стеклянную трубку длиной 100 сантиметров и погрузил ее открытым концом в сосуд с ртутью.
При этом ртуть из трубки вся не вылилась, но, немного опустившись, остановилась на уровне около 76 сантиметров; Торричелли сделал совершенно правильный вывод, что ртуть поддерживается в трубке весом наружного воздуха.
Давление воздуха на поверхность ртути в чашке уравновешивается давлением ртутного столба.
В течение нескольких лет выводы Торричелли не были подтверждены. Наконец, в 1647 году французский ученый Паскаль задумал окончательно выяснить этот вопрос.
Он обратился к своему родственнику Перье, жившему в городе Клермон, у подножья горы Пью-де-Дом, с просьбой проделать необходимые наблюдения.
Просьба Паскаля была выполнена 19 сентября 1648 года, и с этой даты то, что воздух имеет вес, перестало вызывать сомнения.
Уменьшение атмосферного давления с высотой. На каждом последующем; уровне длина расположенного выше столба воздуха укорачивается и величина давления уменьшается
Перье поступил так. Он заготовил две одинаковые трубки Торричелли и, измерив высоту ртутного столба в трубках у подножья горы, оставил одну из них на месте, а с другой поднялся на вершину. На высоте 975 метров он опять измерил высоту ртути в трубке. Оказалось, что на вершине она была на 8 миллиметров ниже, чем у подножья горы.
Изумленный полученным результатом, Перье много раз проверял свои измерения и, только окончательно убедившись в их правильности, спустился вниз. В находившейся внизу трубке ртуть осталась на прежнем уровне. На том же уровне она остановилась и в принесенной сверху трубке.
Таким образом, было окончательно доказано, что воздух имеет вес и поэтому в нижних слоях он давит с большей силой, чем вверху, где над головой наблюдателя остается меньшее его количество. Воздух давит на поверхность Земли с такой же силой, с какой давил бы слой воды толщиной в 10,3 метра.
Вот почему насос герцога Тосканского, поднятый над уровнем воды выше 10 метров, не работал. Ртуть в 13,6 раза тяжелее воды. Поэтому она устанавливалась в трубке Торричелли на высоте около 76 сантиметров (76х13,6=1033,6 сантиметра).
Давлением воздуха объясняется и действие медицинской банки, а также и то, что вода из перевернутого, но закрытого бумажкой стакана не выливается.
Мы не замечаем этого большого веса воздуха, так как человеческий организм приспособился к нему и чувствует себя нормально именно в этих условиях.
Все внутренние органы человека наполнены воздухом, имеющим такое же давление, как и давление атмосферы у поверхности Земли вне нашего организма; это внутреннее давление уравновешивает внешнее.
Поднимаясь высоко в горы или на самолете, человек сильно ощущает уменьшение с высотой давления воздуха (рис. 2) и переносит происходящее при этом его понижение только до известного предела, после которого наступает ощущение удушья или даже смерть.
Рыбы, живущие в океане на больших глубинах, приспособились к еще большему давлению, слагающемуся из веса атмосферы и веса огромной массы воды. Выловленные на больших глубинах и поднятые на поверхность моря, рыбы гибнут: их разрывает внутреннее давление, не уравновешиваемое внешним.
Почему же мы не ощущаем веса воздуха, когда поднимаем наполненное воздухом ведро? Да потому, что мы взвешиваем его в самом же воздухе. Подобно этому, опустив ведро в колодец и наполнив его водой, мы не ощущаем веса воды в ведре. Но достаточно приподнять ведро из воды в воздух, как сразу почувствуется его тяжесть.
Один кубический метр воздуха весит 1,3 килограмма, а вся атмосфера, окружающая земной шар, — 5 300 000 000 000 000 тонн. Как видим, воздух весит очень и очень много.
Вес 1 кубического метра воздуха, равный 1,3 килограмма, мы получаем тогда, когда взвешиваем воздух на уровне моря и при температуре 0°. Чем выше от поверхности Земли, тем плотность воздуха становится меньшей и вес 1 его кубического метра уменьшается.
Так, на высоте 12 километров 1 кубический метр воздуха весит 319 граммов, то есть в четыре раза меньше, чем внизу; на высоте 25 километров — 43 грамма, а на высоте 40 километров — только 4 грамма (рис. 3).
Увеличение плотности воздуха книзу и разрежение его вверху обусловливаются земным притяжением. Но как бы ни был разрежен воздух, он, как газ, заполняет все предоставленное ему пространство и, следовательно, распространяется далеко вверх от поверхности Земли.
До каких же высот простирается земная атмосфера? И можно ли вообще установить ее границу или же плотность воздуха постепенно сходит на нет?
Правильно второе предположение, но тем не менее теоретически мы можем установить границы воздушного океана. Это сделать нетрудно, так как мы знаем вес всей атмосферы, лежащей над нашей головой, и можем вычислить вес кубического метра воздуха на любой высоте.
Убывание плотности воздуха с высотой. Преобладающая масса атмосферы расположена в ее нижних слоях
Если бы воздух на всех высотах имел ту же плотность, что и у поверхности Земли, то средняя высота воздушной оболочки, окружающей земной шар, была бы близка к 8 километрам. Но плотность воздуха с высотой быстро уменьшается, и поэтому высота атмосферы должна быть во много сотен раз больше.
Еще М. В. Ломоносов разбирал вопрос о высоте земной атмосферы. Рассуждал он так. Воздух состоит из бесчисленного количества мельчайших частиц — молекул. Молекулы газа находятся в непрерывном движении, несутся вверх, вниз, в стороны.
Внизу, где воздух плотен и число молекул огромно, они непрестанно сталкиваются между собою и как бы «толкутся» на месте. Чем выше, тем меньше молекул в одном и том же объеме воздуха, и путь, который они пролетают от одного столкновения с соседней молекулой до другого, — длиннее.
Расположенные на больших высотах молекулы воздуха при этом часто летят вниз, к Земле; они падают под влиянием силы тяжести, как и все другие тела. Падение продолжается до столкновения с молекулами, расположенными ниже, в более плотных слоях. Оттолкнувшись от них, падавшая молекула снова летит вверх.
Такое движение — вверх и вниз — все молекулы проделывают бесчисленное количество раз. Но вверх молекула движется только до известного уровня. Этот уровень определяется силой земного притяжения, вследствие которого все тела падают на Землю, движутся по ее поверхности и не уносятся от нее в мировое пространство.
Выскакивают за этот уровень и уходят из атмосферы только те молекулы которые на большой высоте получили от столкновения с соседней молекулой толчок такой силы, которая превышает силу земного притяжения на этой высоте.
Более поздние исследования подтвердили правильность рассуждений М В. Ломоносова и показали, что такая теоретическая граница земной атмосферы лежит над полюсом на высоте 28 тысяч километров, над экватором на высоте 42 тысячи километров, то есть более чем в четыре и в семь раз превышает земной радиус.
Нас, земных жителей, в первую очередь интересует высота тех слоев атмосферы, которые имеют еще измеримую плотность и где совершаются те метеорологические и физические явления, которые мы имеем возможность наблюдать и с которыми мы должны считаться.
С такой точки зрения высота земной атмосферы определится слоем толщиной в 800—1000 километров.
Перье измерял давление атмосферы высотой столбика ртути в трубке Торричелли, определяя длину его в миллиметрах. Такой способ измерения сохранился и поныне.
Современные ртутные барометры в принципе ничем не отличаются от трубки Торричелли.
Они только совершеннее технически, что позволяет производить отсчеты очень точно, улавливая самые незначительные (до 1/10 миллиметра) изменения высоты ртутного столба.
Как мы уже знаем, на уровне моря атмосферное давление в среднем соответствует давлению ртутного столба высотой в 760 миллиметров. Но эта величина не остается постоянной. В разных местах в разное время года и при разной погоде она меняется в широких пределах Крайние отмеченные до сих пор значения давления составляют 680 и 802 миллиметра.
Изменение давления воздуха играет значительную роль в явлениях погоды. Но эта роль все же не решающая. Поэтому и предсказывать «погоду, используя измерение только одного давления, нельзя.
Стало быть, не следует придавать большого значения надписям, имеющимся на некоторых металлических барометрах-анероидах: «буря», «дождь» или «сухо». Мы легко согласимся с этим, если вспомним описанный выше опыт Перье: барометр меняет свои показания не только от состояния погоды, но и от высоты, на которой он сейчас находится.
Это его свойство широко используется в авиации, где по показаниям такого же барометра-анероида (альтиметра) определяют высоту самолета.
Для облегчения отсчетов на шкале альтиметра показана не величина давления, а соответствующая высота.
Для ряда теоретических вычислений значительно удобнее величину давления воздуха выражать не длиной ртутного столба, следовательно, не в миллиметрах, а в единицах давления. В качестве такой единицы принят «бар», равный давлению миллиона дин 2 на 1 квадратный сантиметр, что соответствует давлению ртутного столба длиной 750,1 миллиметра.
В практике применяется одна тысячная часть бара — миллибар. Давление ртутного столба длиной в 1 миллиметр равно 1,333 миллибарам. Соответственно этому 1 миллибар приблизительно равен 0,75 миллиметра ртутного столба.
В настоящее время в метеорологии почти повсеместно применяют миллибары, но так как шкалы большинства барометров сделаны в миллиметрах, то отсчет величины давления с помощью специальных таблиц переводится затем в миллибары.
Плотность воздуха
Перейти к навигации Перейти к поиску
Плотность воздуха или плотности атмосферы , обозначаемое ρ ( греческий : Rho), является масса на единицу объема в атмосфере Земли . Плотность воздуха, как и давление воздуха, уменьшается с увеличением высоты.
Он также изменяется при изменении атмосферного давления, температуры и влажности . При 101,325 кПа (абс) и 15 ° C, воздух имеет плотность приблизительно 1,225 кг / м 3 (или 0.00237 нерасклепанной / фут 3 ), около 1 / однотысячные , что воды в соответствии с ISA ( международный стандарт атмосферы ).
[ необходима цитата ]
Плотность воздуха – это свойство, используемое во многих отраслях науки, техники и промышленности, включая аэронавтику ; [1] [2] [3] гравиметрический анализ ; [4] кондиционирование воздуха [5] промышленность; атмосферные исследования и метеорология ; [6] [7] [8] сельскохозяйственная инженерия (моделирование и отслеживание моделей почва-растительность-атмосферный перенос (SVAT)); [9] [10] [11] и инженерное сообщество, имеющее дело со сжатым воздухом. [12]
В зависимости от используемых измерительных приборов могут применяться различные наборы уравнений для расчета плотности воздуха. Воздух – это смесь газов, и расчеты всегда в большей или меньшей степени упрощают свойства смеси.
Температура [ править ]
При прочих равных условиях более горячий воздух менее плотный, чем более холодный, и поэтому поднимается вверх через более холодный воздух. Это можно увидеть, используя в качестве приближения закон идеального газа .
Сухой воздух [ править ]
Плотность сухого воздуха можно рассчитать с помощью закона идеального газа , выраженного как функция температуры и давления:
ρ знак равно п р s п е c я ж я c Т { displaystyle rho = { frac {p} {R _ { rm {specific}} T}}}
куда:
ρ знак равно { Displaystyle rho =} плотность воздуха (кг / м 3 ) [примечание 1] п знак равно { displaystyle p =} абсолютное давление (Па) [примечание 1] Т знак равно { displaystyle T =} абсолютная температура (K) [примечание 1] р s п е c я ж я c знак равно {displaystyle R_{
m {specific}}=} удельная газовая постоянная для сухого воздуха (Дж / (кг · К)) [примечание 1] .
R s p e c i f i c = R M d {displaystyle R_{
m {specific}}={frac {R}{M_{
m {d}}}}} , Где это универсальная газовая постоянная , и это молярная масса сухого воздуха. Удельная газовая постоянная для сухого воздуха составляет 287,058 Дж / (кг · К) в единицах СИ и 53,35 ( фут · фунт-сила ) / ( фунт · ° R ) в обычных и британских единицах измерения США . Это количество может незначительно варьироваться в зависимости от молекулярного состава воздуха в конкретном месте. R {displaystyle R} M d {displaystyle M_{
m {d}}}
Следовательно:
В следующей таблице показана зависимость плотности воздуха от температуры при 1 атм или 101,325 кПа:
| 35 год | 351,88 | 1,1455 | 403,2 |
| 30 | 349,02 | 1,1644 | 406,5 |
| 25 | 346,13 | 1,1839 | 409,4 |
| 20 | 343,21 | 1,2041 | 413,3 |
| 15 | 340,27 | 1,2250 | 416,9 |
| 10 | 337,31 | 1,2466 | 420,5 |
| 5 | 334,32 | 1,2690 | 424,3 |
| 331,30 | 1,2922 | 428,0 | |
| −5 | 328,25 | 1,3163 | 432,1 |
| −10 | 325,18 | 1,3413 | 436,1 |
| −15 | 322,07 | 1,3673 | 440,3 |
| −20 | 318,94 | 1,3943 | 444,6 |
| −25 | 315,77 | 1,4224 | 449,1 |
Влажный воздух [ править ]
Влияние температуры и относительной влажности на плотность воздуха
Добавление водяного пара к воздуху (делая воздух влажным) снижает плотность воздуха, что на первый взгляд может показаться нелогичным. Это происходит потому, что молярная масса воды (18 г / моль) меньше молярной массы сухого воздуха [примечание 2] (около 29 г / моль). Для любого идеального газа при данной температуре и давлении количество молекул постоянно для определенного объема (см. Закон Авогадро ). Поэтому, когда молекулы воды (водяной пар) добавляются к заданному объему воздуха, молекулы сухого воздуха должны уменьшаться на такое же число, чтобы давление или температура не увеличивались. Следовательно, масса единицы объема газа (его плотность) уменьшается.
Плотность влажного воздуха можно рассчитать, рассматривая его как смесь идеальных газов . В этом случае парциальное давление из водяного пара , как известно , как давление паров . При использовании этого метода погрешность расчета плотности составляет менее 0,2% в диапазоне от –10 ° C до 50 ° C. Плотность влажного воздуха определяется по:
ρ h u m i d a i r = p d R d T + p v R v T = p d M d + p v M v R T {displaystyle
ho _{,mathrm {humid~air} }={frac {p_{d}}{R_{d}T}}+{frac {p_{v}}{R_{v}T}}={frac {p_{d}M_{d}+p_{v}M_{v}}{RT}},} [13]
куда:
ρ h u m i d a i r = {displaystyle
ho _{,mathrm {humid~air} }=} Плотность влажного воздуха (кг / м 3 ) p d = {displaystyle p_{d}=} Парциальное давление сухого воздуха (Па) R d = {displaystyle R_{d}=} Удельная газовая постоянная для сухого воздуха, 287,058 Дж / (кг · К) T = {displaystyle T=} Температура ( K ) p v = {displaystyle p_{v}=} Давление водяного пара (Па) R v = {displaystyle R_{v}=} Удельная газовая постоянная для водяного пара, 461,495 Дж / (кг · К) M d = {displaystyle M_{d}=} Молярная масса сухого воздуха, 0,0289652 кг / моль. M v = {displaystyle M_{v}=} Молярная масса водяного пара, 0,018016 кг / моль. R = {displaystyle R=} Универсальная газовая постоянная , 8,31446 Дж / (К · моль)
Давление водяного пара можно рассчитать по давлению насыщенного пара и относительной влажности . Его находят:
p v = ϕ p s a t {displaystyle p_{v}=phi p_{mathrm {sat} },}
куда:
p v = {displaystyle p_{v}=} Давление паров воды ϕ = {displaystyle phi =} Относительная влажность (%, 0,0-1,0) p s a t = {displaystyle p_{mathrm {sat} }=} Давление насыщенного пара
Давление насыщенного пара воды при любой заданной температуре – это давление пара при относительной влажности 100%. Одна формула – уравнение Тетенса из [14], используемое для определения давления насыщенного пара:
p s a t = 6.1078 × 10 7.5 T T + 237.3 {displaystyle p_{mathrm {sat} }=6.1078 imes 10^{frac {7.5T}{T+237.3}}}
куда:
p s a t = {displaystyle p_{mathrm {sat} }=} Давление насыщенного пара (гПа) T = {displaystyle T=} Температура ( C )
См. Давление водяного пара для других уравнений.
Парциальное давление сухого воздуха определяется с учетом парциального давления , в результате чего: p d {displaystyle p_{d}}
p d = p − p v {displaystyle p_{d}=p-p_{v},}
Где просто обозначает наблюдаемое абсолютное давление . p {displaystyle p}
Вариация с высотой [ править ]
Стандартная атмосфера: p 0 = 101,325 кПа, T 0 = 288,15 K, ρ 0 = 1,225 кг / м 3
Тропосфера [ править ]
Для расчета плотности воздуха как функции высоты требуются дополнительные параметры. Для тропосферы, самой нижней части атмосферы, они перечислены ниже вместе с их значениями в соответствии с Международным стандартом атмосферы , с использованием для расчета универсальной газовой постоянной вместо постоянной для воздуха:
p 0 = {displaystyle p_{0}=} стандартное атмосферное давление на уровне моря, 101325 Па T 0 = {displaystyle T_{0}=} стандартная температура на уровне моря, 288,15 К g = {displaystyle g=} ускорение свободного падения земная поверхность, 9,80665 м / с 2 L = {displaystyle L=} градиент температуры , 0,0065 К / м R = {displaystyle R=} идеальная (универсальная) газовая постоянная, 8,31446 Дж / ( моль · К) M = {displaystyle M=} молярная масса сухого воздуха 0,0289652 кг / моль
Температура на высоте метров над уровнем моря приблизительно рассчитывается по следующей формуле (действительна только в тропосфере , не более чем на ~ 18 км над поверхностью Земли (и ниже от экватора)): h {displaystyle h}
T = T 0 − L h {displaystyle T=T_{0}-Lh,}
Давление на высоте определяется по формуле: h {displaystyle h}
p = p 0 ( 1 − L h T 0 ) g M / R L {displaystyle p=p_{0}left(1-{frac {Lh}{T_{0}}}
ight)^{gM/RL}}
Затем можно рассчитать плотность в соответствии с молярной формой закона идеального газа :
ρ = p M R T = p M R T 0 ( 1 − L h / T 0 ) = p 0 M R T 0 ( 1 − L h T 0 ) g M / R L − 1 {displaystyle
ho ={frac {pM}{RT}},={frac {pM}{RT_{0}(1-Lh/T_{0})}}={frac {p_{0}M}{RT_{0}}}left(1-{frac {Lh}{T_{0}}}
ight)^{gM/RL-1},}
куда:
M = {displaystyle M=} молярная масса R = {displaystyle R=} постоянная идеального газа T = {displaystyle T=} абсолютная температура p = {displaystyle p=} абсолютное давление
Обратите внимание, что плотность у земли равна ρ 0 = p 0 M R T 0 {displaystyle
ho _{0}={frac {p_{0}M}{RT_{0}}}}
Несложно проверить, что выполняется уравнение гидростатики :
d p d h = − g ρ {displaystyle {frac {dp}{dh}}=-g
ho } .
Экспоненциальное приближение [ править ]
Поскольку температура изменяется с высотой внутри тропосферы менее чем на 25%, можно приблизительно указать: L h T 0
Плотность воздуха, значение и примеры
Содержание составных частей практически не зависит от того, в каком месте земного шара взята проба сухого воздуха. Ко второй группе относятся углекислый газ (0,02 – 0,04%) и водяной пар (до 3%).
Содержание случайных составных частей зависит от местных условий: вблизи металлургических заводов к воздуху часто бывают примешаны заметные количества сернистого газа, в местах, где происходит распад органических остатков, – аммиака и т.д.
Помимо различных газов, воздух всегда содержит большее или меньшее количество пыли.
Плотность воздуха представляет собой величину, равную массе газа атмосферы Земли, деленную на единицу объема. Она зависит от давления, температуры и влажности. Существует стандартная величина плотности воздуха – 1,225 кг/м3, соответствующая плотности сухого воздуха при температуре 15oС и давлении 101330 Па.
- Зная из опыта массу литра воздуха при нормальных условиях (1,293 г), можно вычислить тот молекулярный вес, который имел бы воздух, если бы он был индивидуальным газом. Так как грамм-молекула всякого газа занимает при нормальных условиях объем 22,4 л, средний молекулярный вес воздуха равен
- 22,4 × 1,293 = 29.
- Это число – 29 – следует запомнить: зная его, легко рассчитать плотность любого газа по отношению к воздуху.
Плотность жидкого воздуха
При достаточном охлаждении воздух переходит в жидкое состояние. Жидкий воздух можно довольно долго сохранять в сосудах с двойными стенками, из пространства между которыми для уменьшения теплопередачи выкачан воздух. Подобные сосуды используются, например, в термосах.
Свободно испаряющийся при обычных условиях жидкий воздух имеет температуру около (-190oС). Состав его непостоянен, так как азот улетучивается легче кислорода. По мере удаления азота цвет жидкого воздуха изменяется от голубоватого до бледно-синего (цвет жидкого кислорода).
В жидком воздухе легко переходят в твердое состояние этиловый спирт, диэтиловый эфир и многие газы. Если, например, пропускать через жидкий воздух диоксид углерода, то он превращается в белые хлопья, похожие по внешнему виду на снег. Ртуть, погруженная в жидкий воздух, становится твердой и ковкой.
Многие вещества, охлажденные жидким воздухом, резко изменяют свои свойства. Так, чинк и олово становятся настолько хрупкими, что легко превращаются в порошок, свинцовый колокольчик издает чистый звенящий звук, а замороженный резиновый мячик разбивается вдребезги, если уронить его на пол.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! |
Плотность и относительная плотность 2021
Определение плотности воздуха ^
Не так давно сведения о плотности воздуха получали косвенно за счет наблюдений за полярными сияниями, распространением радиоволн, метеорами. С момента появления искусственных спутников Земли плотность воздуха начали вычислять благодаря данным, полученным от их торможения.
Еще один метод заключается в наблюдениях за расплыванием искусственных облаков из паров натрия, создаваемых метеорологическими ракетами. В Европе плотность воздуха у поверхности Земли составляет 1,258 кг/м3, на высоте пяти км — 0,735, на высоте двадцати км — 0,087, на высоте сорока км — 0,004 кг/м3.
Различают два вида плотности воздуха: массовая и весовая (удельный вес).
Как выбрать освежители воздуха для комнаты, какие они бывают?
Если вам стало тяжело дышать, какие могут быть причины этого явления? Об этом можно прочитать здесь. Бережем свое здоровье!
Исследования Ньютона
Если задуматься, то такие явления, перечисленные выше, могут показаться непонятными. Ведь как сухой воздух может быть тяжелее того, который насыщен влагой? А именно водой в газообразном состоянии.
Но это парадоксальное явление давно доказали ученые, да еще и подтвердили многими исследованиями. Первый, кто об этом начал говорить, был Исаак Ньютон. Все свои мысли и доводы он написал в книге «Оптика».
Ученый говорил о том, что именно плотность влажного воздуха ниже, чем у сухого. В 1717 году эта книга вышла в свет в Лондоне
Но, к сожалению, гипотезы известного ученого не взяли во внимание, «Оптика» не имела большого успеха
Что такое относительная плотность по воздуху? ^
Следует принять во внимание, что вес воздуха – это величина изменчивая и меняется в зависимости от различных условий, таких как географическая широта и сила инерции, которая возникает при вращении Земли вокруг своей оси. На полюсах вес воздуха на 5% больше, чем в зоне экватора.
Массовая плотность воздуха – это масса 1 м3 воздуха, обозначаемая греческой буквой ρ. Как известно, масса тела – величина постоянная. За единицу массы принято считать массу гири из иридистой платины, которая находится в Международной палате мер и весов в Париже.
Массовая плотность воздуха ρ вычисляется по следующей формуле: ρ = m / v. Здесь m – масса воздуха, измеряемая в кг×с2/м; ρ – его массовая плотность, измеряемая в кгс×с2/м4.
Массовая и весовая плотности воздуха находятся в зависимости: ρ = γ / g, где g – коэффициент ускорения свободного падения, равный 9,8 м/с². Откуда следует, что массовая плотность воздуха при стандартных условиях равна 0,1250 кг×с2/м4.
Примечания
- Существуют также поверхностная плотность (отношение массы к площади) и
линейная плотность
(отношение массы к длине), применяемые соответственно к плоским (двумерным) и вытянутым (одномерным) объектам.
- Подразумевается также, что область стягивается к точке, то есть, не только её объём стремится к нулю (что могло бы быть не только при стягивании области к точке, но, например, к отрезку), но также стремится к нулю и её диаметр (максимальный линейный размер).
- Агекян Т. А. Расширение Вселенной. Модель Вселенной // Звёзды, галактики, Метагалактика. 3-е изд. / Под ред. А. Б. Васильева. — М.: Наука, 1982. — 416 с. — С. 249.
- , p. 158.
- , p. 136.
- , p. 96.
- , p. 160.
- , p. 138.
- , p. 198.
- , p. 319.
- ↑ , p. 165.
- , p. 179.
- , p. 163.
- , p. 141.
- , p. 67.
- , p. 151.
- , p. 111.
- , p. 60.
- , p. 108.
- , p. 57.
- , p. 313.
- , p. 105.
- , p. 50.
- , p. 168.
- , p. 101.
- , p. 54.
- , p. 134.
- , p. 98.
- , p. 47.
Как плотность воздуха зависит от температуры? ^
При изменении барометрического давления и температуры плотность воздуха изменяется. Исходя из закона Бойля-Мариотта, чем больше давление, тем больше будет плотность воздуха. Однако с уменьшением давления с высотой, уменьшается и плотности воздуха, что привносит свои коррективы, в результате чего закон изменения давления по вертикали становится сложнее.
Уравнение, которое выражает данный закон изменения давления с высотой в атмосфере, находящейся в покое, называется основным уравнением статики.
Оно гласит, что с увеличением высоты давление изменяется в меньшую сторону и при подъеме на одну и ту же высоту уменьшение давления тем больше, чем больше сила тяжести и плотность воздуха.
Важная роль в этом уравнении принадлежит изменениям плотности воздуха. В итоге можно сказать, что чем выше подниматься, тем меньше будет падать давление при подъеме на одинаковую высоту.
Плотность воздуха от температуры зависит следующим образом: в теплом воздухе давление уменьшается менее интенсивно, чем в холодном, следовательно, на одинаково равной высоте в теплой воздушной массе давление более высокое, чем в холодной.
При изменяющихся значениях температуры и давления массовая плотность воздуха вычисляется по формуле: ρ = 0,0473хВ / Т. Здесь В – это барометрическое давление, измеряемое в мм ртутного столба, Т — температура воздуха, измеряемая в Кельвинах.
Как выбирают газовые обогреватели для дачи, по каким характеристикам, параметрам?
Что такое промышленный осушитель сжатого воздуха? Читайте про это здесь, наиболее интересная и актуальная информация.
Какие сейчас цены на озонотерапию? Вы узнаете об этом в данной статье: https://about-air.ru/sostav-vozduha/ozon/ozonoterapiya-otzyvy.html. Отзывы, показания и противопоказания при озонотерапии.
Возможные проблемы с зарядкой
Розетки на территории страны не всегда имеют хорошее качество. Часто случается такое, что специальный штекер в нее входит, но зажимания контактами не происходит. Устройство в розетке держится плохо, что создает неустойчивый контакт. Это может спровоцировать порчу техники.
Туристы решают эту проблему путем прижатия вилки чем-то тяжелым. Данные методы могут спровоцировать возникновение пожара. Делать такое не рекомендуется. Чтобы воспользоваться каким-либо электрическим прибором, необходимо приобрести переходник в ближайшем супермаркете.
Цены на них не высокие.
Как измеряется плотность паров по воздуху? ^
Также плотность определяется и влажностью воздуха. Наличие водяных поров приводит к уменьшению плотности воздуха, что объясняется низкой молярной массой воды (18 г/моль) на фоне молярной массы сухого воздуха (29 г/моль). Влажный воздух можно рассмотреть как смесь идеальных газов, в каждом из которых комбинация плотностей позволяет получить требуемое значение плотности для их смеси.
Такая, своего рода, интерпретация позволяет определять значения плотности с уровнем погрешности менее 0,2% в диапазоне температур от −10 °C до 50 °C. Плотность воздуха позволяет получить величину его влагосодержания, которая вычисляется путем деления плотности водяного пара (в граммах), который содержится в воздухе, на показатель плотности сухого воздуха в килограммах.
Основное уравнение статики не позволяет решать постоянно возникающие практические задачи в реальных условиях изменяющейся атмосферы. Поэтому его решают при различных упрощенных предположениях, которые соответствуют фактическим реальным условиям, за счет выдвижения ряда частных предположений.
Основное уравнение статики дает возможность получить значение вертикального градиента давления, который выражает изменение давления при подъеме или спуске на единицу высоты, т. е. изменение давления на единицу расстояния по вертикали.
Вместо вертикального градиента нередко используют обратную ему величину — барическую ступень в метрах на миллибар (иногда еще встречается устаревший вариант термина «градиент давления» — барометрический градиент).
Низкая плотность воздуха определяет незначительное сопротивление передвижению. Многими наземными животными, в ходе эволюции, использовались экологические выгоды этого свойства воздушной среды, за счет чего они приобрели способность к полету. 75% всех видов наземных животных способны к активному полету. По большей части это насекомые и птицы, но встречаются млекопитающие и рептилии.
Видео на тему «Определение плотности воздуха»
Практическое применение
Из учебников химии и физики вычисляют уровень плотности по формуле. Но также это можно сделать, используя онлайн-систему.
Значение показателя
Окружающий мир состоит из разных веществ.
Скамейка в парке или баня за городом сооружены из древесины, подошва утюга, сковорода выполнены из металла, покрышка колеса, велосипеда — из резины. Каждый предмет имеет свой вес.
Черные дыры Вселенной составляют наибольшую плотность 1014 кг/м3. Самый низкий показатель имеет область между Галактиками (2•10−31—5•10−31 кг/м³).
Таблица плотности веществ
| Вещество | Плотность (кг/м3) |
| Сухой воздух | 1,293 |
| Металлы | |
| Осмий | 22,61 |
| Родий | 12,41 |
| Иридий | 22,56 |
| Плутоний | 19,84 |
| Палладий | 12,02 |
| Свинец | 11,35 |
| Платина | 19,59 |
| Золото | 19,30 |
| Сталь | 7,8 |
| Алюминий | 2,7 |
| Медь | 8,94 |
| Газы | |
| Азот | 1,25 |
| Аммиак | 0,771 |
| Аргон | 1,784 |
| Жидкий водород | 70 |
| Гелий в жидком состоянии | 130 |
| Водород | 0,09 |
| Водяной пар | 0,598 |
| Воздух | 1,293 |
| Хлор | 3,214 |
| О2 | 1,429 |
| Углекислый газ | 1,977 |
| Остальные вещества | |
| Тело человека | На вдохе 940-990, при выдохе — 1010-1070 |
| Пресная вода | 1000 |
| Солнце | 1410 |
| Гранит | 2600 |
| Земля | 5520 |
| Железо | 7874 |
| Бензин | 710 |
| Керосин | 820 |
| Молоко | 1040 |
| Этанол | 789 |
| Ацетон | 792 |
| Морская вода | 1030 |
| Древесина | |
| Пихта | 0,39 |
| Ива | 0,46 |
| Ель | 0,45 |
| Сосна | 0,52 |
| Дуб | 0,69 |
П металлов изменяется от минимального значения у лития, который легче Н2О, до максимального значения у осмия, который тяжелее драгоценных металлов.
Размножение
Этот сорт розы, как и другие, может размножаться двумя способами: черенкованием и делением куста. Чаще всего используют первый способ, ведь куст растет достаточно долго. В исключительных случаях его разделяют на 2 части. При этом роза должна быть старше 5 лет. После такой процедуры растение часто замедляет свой рост и приостанавливает цветение.
Черенкование – наиболее простой и доступный метод размножения роз. Для получения хорошего черенка необходимо срезать побеги длиной до 20 см. Заготовки обязательно должны быть со здоровых побегов, образовавшихся этим летом. Срез делают под наклоном.
Сталь ШХ15 – характеристики и применение
Подготовленные черенки необходимо высадить в увлажненную почву под банку или пластиковую бутылку. Укоренившиеся черенки необходимо высадить следующей весной.
Блэк Баккара ценится многими садоводами. Она отлично растет в тени, поэтому вы можете ее расположить в любом уголке вашего сада. Кроме того, черная роза отлично чувствует себя в горшках и контейнерах. Потому это растение можно выращивать даже в комнатных условиях.
Основные параметры воздуха, классы фильтров, расчет мощности калорифера, стандарты и нормативные документы, таблица физических величин – УКЦ
ТЕМПЕРАТУРА . Измеряется как в Кельвинах (К), так и в градусах Цельсия (°С). Размер градуса Цельсия и размер кельвина один и тот же для разности температур. Соотношение между температурами:
t = T — 273,15 K,
где t — температура, °С, T — температура, K.
ДАВЛЕНИЕ . Давление влажного воздуха p и его составляющих измеряется в Па (Паскаль) и кратных единицах (кПа, ГПа, МПа).
- Барометрическое давление влажного воздуха pб равно сумме парциальных давлений сухого воздуха pв и водяного пара pп :
- pб = pв + pп
- ПЛОТНОСТЬ . Плотность влажного воздуха ρ, кг/м3, представляет собой отношение массы воздушно-паровой смеси к объему этой смеси:
- ρ = M/V = Mв /V + Mп /V
- Плотность влажного воздуха может определяться по формуле
- ρ = 3,488 pб /T — 1,32 pп /T
УДЕЛЬНЫЙ ВЕС . Удельный вес влажного воздуха γ — это отношение веса влажного воздуха к занимаемому им объему, Н/м3. Плотность и удельный вес связаны между собой зависимостью
ρ = γ /g,
где g — ускорение свободного падения, равное 9.81 м/с2.
ВЛАЖНОСТЬ ВОЗДУХА . Содержание в воздухе водяного пара. характеризуется двумя величинами: абсолютной и относительной влажностью.
Абсолютная
влажность воздуха . количество водяного пара, кг или г, содержащегося в 1 м3 воздуха.
Относительная
влажность воздуха φ, выраженная в % . отношение парциального давления водяного пара pп, содержащегося в воздухе, к парциальному давлению водяного пара в воздухе при полном его насыщении водяными парами pп.н.:
φ = (pп /pп.н. ) 100%
Парциальное давление водяного пара в насыщенном влажном воздухе может быть определено из выражения
lg pп.н. = 2,125 + (156 + 8,12tв.н. )/(236 + tв.н. ),
где tв.н. — температура насыщенного влажного воздуха, °С.
ТОЧКА РОСЫ . Температура, при которой парциальное давление водяного пара pп , содержащегося во влажном воздухе, равно парциальному давлению насыщеного водяного пара pп.н. при той же температуре. При температуре росы начинается конденсация влаги из воздуха.
- ВЛАГОСОДЕРЖАНИЕ . Влагосодержание влажного воздуха d представляет собой отношение массы водяного пара Mп во влажном воздухе к массе сухой части влажного воздуха Mв :
- d = Mп / Mв
- Влагосодержание влажного воздуха, г/кг, может быть выражено через давление влажного воздуха и его составляющих и относительную влажность:
d = 622pп / (pб — pп ) = 6,22φpп.н.(pб — φpп.н. /100)
- УДЕЛЬНАЯ ТЕПЛОЕМКОСТЬ . Удельная теплоемкость влажного воздуха c, кДж/(кг * °С) — это количество теплоты, требуемой для нагрева 1 кг смеси сухого воздуха и водяных паров на 10 и отнесенное к 1 кг сухой части воздуха:
- с = св + сп d /1000,
- где cв — средняя удельная теплоемкость сухого воздуха, принимаемая в интервале температур 0-1000С равной 1,005 кДж/(кг * °С); сп — средняя удельная теплоемкость водяного пара, равная 1,8 кДж/(кг * °C). Для практических расчетов при проектировании систем отопления, вентиляции и кондиционирования воздуха допускается применять удельную теплоемкость влажного воздуха с = 1,0056 кДж/(кг * °C) (при температуре 0°С и барометрическом давлении 1013,3 ГПа)
- УДЕЛЬНАЯ ЭНТАЛЬПИЯ . Удельная энтальпия влажного воздуха — это энтальпия I, кДж, отнесенная к 1 кг массы сухого воздуха:
- I = 1,005t + (2500 + 1,8068t) d / 1000, или I = ct + 2.5d
- КОЭФФИЦИЕНТ ОБЪЕМНОГО РАСШИРЕНИЯ . Температурный коэффициент объемного расширения
- α = 0,00367 °C-1
- или α = 1/273 °C-1.
- ПАРАМЕТРЫ СМЕСИ .
- Температура смеси воздуха
- tсм = (M1 t1 + M2 t2 ) / (M1 + M2 )
- Влагосодержание смеси воздуха
- dсм = (M1 d1 + M2 d2 ) / (M1 + M2 )
- Удельная энтальпия смеси воздуха
- Iсм = (M1 I1 + M2 I2 ) / (M1 + M2 )
- где M1, M2 — массы смешиваемого воздуха
КЛАССЫ ФИЛЬТРОВ
| Применение | Класс очистки | Степень очистки | ||||
| Стандарты | DIN 24185 DIN 24184 | EN 779 | EUROVENT 4/5 | EN 1882 | ||
| Фильтр для грубой очистки с невысокими требованиями к чистоте воздуха | Грубая очистка | EU1 | G1 | EU1 | — | A% |
| Фильтр, применяемый при высокой концентрации пыли с грубой очисткой от нее, Кондиционирование воздуха и вытяжная эентиляция с невысокими требованиями к чистоте воздуха в помещении. | 65 | |||||
| EU2 | G2 | EU2 | — | 80 | ||
| EU3 | G3 | EU3 | — | 90 | ||
| EU4 | G4 | EU4 | — | |||
| Сепарирование тонкой пыли в вентиляционном оборудовании, применяемом в помещениях с высокими требованиями к шстоте воздуха. Фильтр для очень тонкой фильтрации. Вторая сепень очистки (доочистка) в помещениях со средними требованиями к чистоте воздуха. | Тонкая очистка | EU5 | EU5 | EU5 | — | E% |
| 60 | ||||||
| EU6 | EU6 | EU6 | — | 80 | ||
| EU7 | EU7 | EU7 | — | 90 | ||
| EU8 | EU8 | EU8 | — | 95 | ||
| EU9 | EU9 | EU9 | — | |||
| Очистка от сверхтонкой пыли. Применяется в помещениях с повышенными требованиями к чистоте воздуха (“чистая комната”). Финишная очистка воздуха в помещенияхс прецизионной техникой, хирургических блоках, реанимационных палатах, в фармацевтической промышленности. | Особо тонкая очистка | — | — | — | EU5 | С% |
| 97 | ||||||
| — | — | — | EU6 | 99 | ||
| — | — | — | EU7 | 99,99 | ||
| — | — | — | EU8 | 99,999 |
РАСЧЕТ МОЩНОСТИ КАЛОРИФЕРА
| Подогрев, °С | ||||||||||
| м3/ч | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 100 | 0.2 | 0.3 | 0.5 | 0.7 | 0.8 | 1.0 | 1.2 | 1.4 | 1.5 | 1.7 |
| 200 | 0.3 | 0.7 | 1.0 | 1.4 | 1.7 | 2.0 | 2.4 | 2.7 | 3.0 | 3.4 |
| 300 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.6 | 4.1 | 4.6 | 5.1 |
| 400 | 0.7 | 1.4 | 2.0 | 2.7 | 3.4 | 4.1 | 4.7 | 5.4 | 6.1 | 6.8 |
| 500 | 0.8 | 1.7 | 2.5 | 3.4 | 4.2 | 5.1 | 5.9 | 6.8 | 7.6 | 8.5 |
| 600 | 1.0 | 2.0 | 3.0 | 4.1 | 5.1 | 6.1 | 7.1 | 8.1 | 9.1 | 10.1 |
| 700 | 1.2 | 2.4 | 3.6 | 4.7 | 5.9 | 7.1 | 8.3 | 9.5 | 10.7 | 11.8 |
| 800 | 1.4 | 2.7 | 4.1 | 5.4 | 6.8 | 8.1 | 9.5 | 10.8 | 12.2 | 13.5 |
| 900 | 1.5 | 3.0 | 4.6 | 6.1 | 7.6 | 9.1 | 10.7 | 12.2 | 13.7 | 15.2 |
| 1000 | 1.7 | 3.4 | 5.1 | 6.8 | 8.5 | 10.1 | 11.8 | 13.5 | 15.2 | 16.9 |
| 1100 | 1.9 | 3.7 | 5.6 | 7.4 | 9.3 | 11.2 | 13.0 | 14.9 | 16.7 | 18.6 |
| 1200 | 2.0 | 4.1 | 6.1 | 8.1 | 10.1 | 12.2 | 14.2 | 16.2 | 18.3 | 20.3 |
| 1300 | 2.2 | 4.4 | 6.6 | 8.8 | 11.0 | 13.2 | 15.4 | 17.6 | 19.8 | 22.0 |
| 1400 | 2.4 | 4.7 | 7.1 | 9.5 | 11.8 | 14.2 | 16.6 | 18.9 | 21.3 | 23.7 |
| 1500 | 2.5 | 5.1 | 7.6 | 10.1 | 12.7 | 15.2 | 17.8 | 20.3 | 22.8 | 25.4 |
| 1600 | 2.7 | 5.4 | 8.1 | 10.8 | 13.5 | 16.2 | 18.9 | 21.6 | 24.3 | 27.1 |
| 1700 | 2.9 | 5.7 | 8.6 | 11.5 | 14.4 | 17.2 | 20.1 | 23.0 | 25.9 | 28.7 |
| 1800 | 3.0 | 6.1 | 9.1 | 12.2 | 15.2 | 18.3 | 21.3 | 24.3 | 27.4 | 30.4 |
| 1900 | 3.2 | 6.4 | 9.6 | 12.8 | 16.1 | 19.3 | 22.5 | 25.7 | 28.9 | 32.1 |
| 2000 | 3.4 | 6.8 | 10.1 | 13.5 | 16.9 | 20.3 | 23.7 | 27.1 | 30.4 | 33.8 |
СТАНДАРТЫ И НОРМАТИВНЫЕ ДОКУМЕНТЫ
СНиП 2.01.01-82 — Строительная климатология и геофизика
Информация о климатических условиях конкретных территорий.