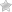Биологические науки изучают живые организмы не только «изнутри», но также исследуют особенности их взаимодействия друг с другом и окружающей средой. Не является исключением и генетика. Одним из интереснейших её направлений является популяционная генетика. Как следует из названия, это направление генетической науки изучает особенности наследственности и изменчивости на уровне популяций. Но для начала давайте разберемся, что же такое популяция…
Что такое популяция
Популяция – это термин, который происходит от латинского — populatio, т.е. население. Он обозначает совокупность организмов относящихся к одному виду, которые длительное время обитают на определённой территории (имеют общий ареал обитания) и полностью либо частично изолированны от особей других аналогичных групп того же вида.
Безусловно для понимания данного термина следует привести пример. И, как говорится, будем «тренироваться, на кошках». Поэтому в качестве примера популяции рассмотрим бездомных кошек в городе.
Они все принадлежат к одному виду и имеют общий ареал обитания (город), и попасть в другой город для них достаточно проблематично, так как для этого необходимо покрыть огромное расстояние, что обуславливает их относительную изоляцию.
Популяция
Для чего нужна популяционная генетика
Интерес изучения генетики на популяционном уровне заключается в том, что через популяционный уровень осуществляется генетическая преемственность поколений, а также регуляция таких биологически важных свойств, как численность, плодовитость, устойчивость к заболеваниям и пр.
Таким образом, популяционная генетика — это раздел генетической науки, который изучает распределение частот аллелей (различных форм одного и того же гена, расположенных в одинаковых участках хромосом), а также их изменение под влиянием движущих сил эволюции, определяющих генетическую структуру популяции.
Она является одним из главных элементов синтетической теории эволюции. Механизмы, которые определяют генетическую структуру популяций, можно разделить на две группы:
- поддерживающие равновесие,
- те, которые, его нарушают.
К первым относятся естественный отбор и дрейф генов, а ко вторым мутагенез и поток генов. При этом естественный отбор и мутагенез оказывают систематическое воздействие, а дрейф и поток генов – случайное. Тем самым, популяционная генетика объясняет процессы адаптации и видообразования.
Аллельные гены
В общем исследования в области генетики популяций можно условно разделить на два направления:
- описание генетического состава популяций
- анализ причин изменения генофонда популяции.
Закон Харди-Вайнберга
Рассмотрение каждого из механизмов определяющих генетическую структуру популяции, заслуживает отдельной статьи, но понимание их невозможно без рассмотрения ключевого закона популяционной генетики – закона Харди-Вайнберга или закона равновесного состояния. На нем и остановим своё внимание.
Итак, механизмы этого закона был открыты в 1908 г. английским математиком Харди (Hardy) и немецким врачом (Weinberg) независимо друг от друга.
Для его понимания рассмотрим такое понятие как случайное скрещивание.
Случайное скрещивание – это скрещивание при котором генетическая структура особей не влияет на вероятность формирования брачных пар между ними. Таким образом, в случайно скрещивающихся популяциях частота спариваний носителей различных генотипов пропорциональна доле, частотности данных генотипов в популяции.
Итак, согласно закону Харди-Вайнберга при отсутствии элементарных эволюционных процессов (естественного отбора, мутаций, дрейфа генов и миграции) частоты генов из поколения в поколение остаются неизменными.
Соответственно если скрещивания случайны, частота генотипа связана простым квадратичным соотношением с частотой генов (аллелей).
Если речь идет об аутосомном локусе, то равновесие генов достигается за одно поколение, и если дополнительные вмешательства, нарушающие структуру популяции, отсутствуют, сохраняется во всех последующих поколениях. Если же мы говорим о сцепленных с полом локусах, равновесные частоты генотипов устанавливаются постепенно.
Годфри Харолд Харди (1877-1947)
- Таким образом равновесные частоты генотипов определяются произведениями частот соответствующих аллелей. В случае наличия только двух аллелей А (с частотой встречаемости p) и а (с частотой – q), частоты каждого их трех возможных генотипов будут выражены уравнением:
- (p + q)2 = p2 + 2pq + q2 = 1.
- A a AA Aa aa
- Если мы говорим о трех аллелях А, а, А’ с частотами p, q, r, формула будет иметь вид:
- (p + q + r)2 = p2 + q2 + r2 + 2pq + 2pr + 2qr = 1.
- А a А’ АА aa А’А’ Аa АА’ aА’
Этот прием возведения в квадрат многочлена может быть использован для определения равновесных частот генотипов при любом числе аллелей. При этом сумма частот генотипов (как и аллелей) всегда должна равняться единице.
Популяционная генетика
Задачи на закон Харди-Вайнберга не всегда просто даются начинающим генетикам. Помните, что Вы всегда можете обратиться к нашим авторам за квалифицированной и своевременной помощью! Сделайте процесс своего обучения приятным и легким вместе с Zaochnik!
История права Харди-Вайнберга, допущения и решенные проблемы / биология
закон Харди-Вайнберга, также называемый принцип Харди-Вайнберга или равновесие, состоит из математической теоремы, которая описывает гипотетическую диплоидную популяцию с половым размножением, которое не эволюционирует – частоты аллелей не меняются от поколения к поколению.
Этот принцип предполагает пять условий, необходимых для того, чтобы популяция оставалась постоянной: отсутствие потока генов, отсутствие мутаций, случайное спаривание, отсутствие естественного отбора и бесконечно большой размер популяции. Таким образом, в отсутствие этих сил население остается в равновесии.
Когда ни одно из вышеприведенных предположений не выполняется, происходит изменение. По этой причине естественный отбор, мутация, миграция и генетический дрейф являются четырьмя эволюционными механизмами..
Согласно этой модели, когда аллельные частоты популяции р и Q, генотипические частоты будут р2, 2рд и Q2.
Мы можем применить равновесие Харди-Вайнберга при расчете частот некоторых представляющих интерес аллелей, например, для оценки доли гетерозигот в человеческой популяции. Мы также можем проверить, находится ли население в равновесии или нет, и предложить гипотезы о том, что силы действуют в указанной популяции..
индекс
- 1 Историческая перспектива
- 2 Популяционная генетика
- 3 Каков баланс Харди-Вайнберга?
- 4 Пример
- 4.1 Первое поколение мышей
- 4.2 Второе поколение мышей
- 5 предположений о равновесии Харди-Вайнберга
- 5.1 Население бесконечно большое
- 5.2 Нет потока генов
- 5.3 Нет мутаций
- 5.4 Случайное спаривание
- 5.5 Нет выбора
- 6 Проблемы решены
- 6.1 Частота носителей фенилкетонурии
- 6.2 Ответ
- 6.3 Является ли следующая популяция в равновесии Харди-Вайнберга??
- 6.4 Популяция бабочек
- 7 ссылок
Историческая перспектива
Принцип Харди-Вайнберга родился в 1908 году и обязан своим именем своим ученым Г.Х. Харди и В. Вайнберг, которые самостоятельно пришли к одним и тем же выводам.
До этого другой биолог по имени Удни Йоль занимался этой проблемой в 1902 году. Йоль начал с набора генов, в которых частоты обоих аллелей были 0,5 и 0,5. Биолог показал, что частоты сохранялись в течение следующих поколений.
Хотя Йоль пришел к выводу, что частоты аллелей можно поддерживать стабильными, их интерпретация была слишком буквальной. Он полагал, что единственное состояние равновесия было найдено, когда частоты соответствовали значению 0,5..
Йоль горячо обсуждал результаты своего романа с Р.С. Пуннетт – широко известен в области генетики благодаря изобретению знаменитой «коробки Пуннетта». Хотя Паннетт знал, что Йоль был неправ, он не нашел математического способа доказать это..
Поэтому Паннетт связался со своим математическим другом Харди, которому удалось немедленно решить его, повторив вычисления, используя общие переменные, а не фиксированное значение 0,5, как это сделал Йоль..
Популяционная генетика
Популяционная генетика направлена на изучение сил, которые приводят к изменению частот аллелей в популяциях, объединяя теорию эволюции Чарльза Дарвина посредством естественного отбора и менделевской генетики. В настоящее время его принципы обеспечивают теоретическую основу для понимания многих аспектов эволюционной биологии..
Одной из важнейших идей популяционной генетики является взаимосвязь между изменениями относительного обилия признаков и изменениями относительного обилия аллелей, которые их регулируют, что объясняется принципом Харди-Вайнберга. Фактически, эта теорема обеспечивает концептуальную основу для популяционной генетики..
В свете популяционной генетики концепция эволюции заключается в следующем: изменение частот аллелей на протяжении поколений. Когда нет изменений, нет эволюции.
Каков баланс Харди-Вайнберга?
Равновесие Харди-Вайнберга – это нулевая модель, которая позволяет нам определять поведение частот генов и аллелей на протяжении поколений. Другими словами, это модель, которая описывает поведение генов в популяциях в ряде конкретных условий..
обозначение
В теореме Харди-Вайнберма аллельная частота (доминантный аллель) представлен буквой р, в то время как аллельная частота в (рецессивный аллель) представлен буквой Q.
Ожидаемые генотипические частоты р2, 2рд и Q2, для доминантного гомозиготы (А.А.), гетерозиготный (Aa) и рецессивный гомозигот (аа) соответственно.
Если в этом локусе только два аллеля, сумма частот двух аллелей обязательно должна быть равна 1 (p + q = 1). Биноминальное расширение (p + q)2 представляют генотипические частоты р2 + 2pq + q2 = 1.
пример
В популяции индивиды, которые интегрируют это, пересекают друг друга, чтобы дать начало потомству. В целом, мы можем указать на наиболее важные аспекты этого репродуктивного цикла: производство гамет, слияние их с образованием зиготы и развитие зародыша с образованием нового поколения..
Представьте, что мы можем проследить процесс менделевских генов в упомянутых событиях. Мы делаем это потому, что хотим знать, будет ли аллель или генотип увеличивать или уменьшать частоту и почему это так.
Чтобы понять, как изменяются частоты генов и аллелей в популяции, мы будем следить за производством гамет у мышей. В нашем гипотетическом примере спаривание происходит случайным образом, где все сперматозоиды и яйца случайно перемешаны.
В случае мышей это предположение неверно и является лишь упрощением для облегчения расчетов. Однако в некоторых группах животных, таких как определенные иглокожие и другие водные организмы, гаметы выбрасываются и сталкиваются случайно..
Первое поколение мышей
Теперь давайте сосредоточим наше внимание на конкретном локусе с двумя аллелями: и в. Следуя закону, провозглашенному Грегором Менделем, каждая гамета получает аллель из локуса A. Предположим, что 60% яйцеклеток и сперматозоидов получают аллель , в то время как остальные 40% получили аллель в.
Из-за этого частота аллеля 0,6 и аллель в составляет 0,4. Эта группа гамет будет найдена случайным образом, чтобы вызвать зиготу. Какова вероятность того, что они образуют каждый из трех возможных генотипов? Для этого мы должны умножить вероятности следующим образом:
генотип А.А.: 0,6 х 0,6 = 0,36.
генотип Aa: 0,6 х 0,4 = 0,24. В случае гетерозиготы существуют две формы, в которых он может возникать. Первое, что сперма несет аллель и яйцеклетка аллель в, или обратный случай, сперма в и яйцеклетка . Поэтому мы добавляем 0,24 + 0,24 = 0,48.
генотип аа: 0,4 х 0,4 = 0,16.
Второе поколение мышей
Теперь представьте, что эти зиготы развиваются и становятся взрослыми мышами, которые снова будут производить гамет. Будем ли мы ожидать, что частоты аллелей будут такими же или отличными от предыдущего поколения??
Генотип А.А. будет производить 36% гамет, в то время как гетерозиготы будут производить 48% гамет, а генотип аа 16%.
- Чтобы вычислить новую частоту аллеля, мы добавляем частоту гомозиготы плюс половину гетерозиготы следующим образом:
- Все частоты : 0,36 + ½ (0,48) = 0,6.
- Все частоты в: 0,16 + ½ (0,48) = 0,4.
Если мы сравним их с начальными частотами, мы обнаружим, что они идентичны. Следовательно, согласно концепции эволюции, поскольку нет изменений частоты аллелей на протяжении поколений, популяция находится в равновесии – она не эволюционирует.
Предположения о равновесии Харди-Вайнберга
Каким условиям должна удовлетворять предыдущая популяция, чтобы частота их аллелей оставалась постоянной при прохождении поколений? В модели равновесия Харди-Вайнберга популяция, которая не эволюционирует, соответствует следующим предположениям:
Население бесконечно большое
Популяция должна быть очень большой, чтобы избежать стохастических или случайных эффектов дрейфа генов..
Когда популяции малы, эффект дрейфа генов (случайные изменения частоты аллелей от одного поколения к другому) из-за ошибки выборки значительно выше и может привести к фиксации или потере определенных аллелей.
Там нет потока генов
Миграции не существуют в популяции, поэтому они не могут достигать или оставлять аллели, которые могут изменять частоты генов.
Нет мутаций
Мутации – это изменения в последовательности ДНК, которые могут иметь разные причины. Эти случайные изменения модифицируют генофонд в популяции путем введения или устранения генов в хромосомах..
Случайное спаривание
Смешение гамет должно быть сделано случайным образом – как и предположение, которое мы используем в примере с мышами. Следовательно, не должно быть выбора пары среди отдельных лиц в популяции, включая инбридинг (размножение родственных лиц).
Когда спаривание не является случайным, оно не вызывает изменения частот аллелей от одного поколения к другому, но может генерировать отклонения от ожидаемых генотипических частот.
Там нет выбора
Не существует дифференциального репродуктивного успеха у индивидуумов с разными генотипами, которые могут изменять частоты аллелей в популяции.
Другими словами, в гипотетической популяции все генотипы имеют одинаковую вероятность размножения и выживания.
Когда население не соответствует этим пяти условиям, результатом является эволюция. Логично, что естественные популяции не соответствуют этим предположениям. Поэтому модель Харди-Вайнберга используется в качестве нулевой гипотезы, которая позволяет нам делать приблизительные оценки частот генов и аллелей..
Помимо отсутствия этих пяти условий, существуют и другие возможные причины, по которым население не находится в равновесии.
Один из них происходит, когда локусы связаны с полом или явлениями искажения в сегрегации или мейотический драйв (когда каждая копия гена или хромосомы не передается с равной вероятностью следующему поколению).
Проблемы решены
Частота фенилкетонурии носителей
По оценкам, в Соединенных Штатах у одного из 10000 новорожденных есть состояние, которое называется фенилкетонурия..
Это расстройство выражается только у рецессивных гомозигот при нарушении обмена веществ. Зная эти данные, какова частота носителей заболевания в популяции??
ответ
Чтобы применить уравнение Харди-Вайнберга, мы должны предположить, что выбор партнера не связан с геном, связанным с патологией, и нет инбридинга..
Кроме того, мы предполагаем, что в Соединенных Штатах нет миграционных явлений, нет новых мутаций фенилкетонурии, а вероятность размножения и выживания одинакова для генотипов..
Если вышеупомянутые условия выполняются, мы можем использовать уравнение Харди-Вайнберга для выполнения расчетов, имеющих отношение к проблеме.
Мы знаем, что заболевание случается каждые 10 000 рождений, поэтому Q2 = 0,0001 и частота рецессивного аллеля будет квадратным корнем из этого значения: 0,01.
в качестве р = 1 – Q, мы должны р Это 0,99. Теперь у нас есть частота обоих аллелей: 0,01 и 0,99. Частота носителей относится к частоте гетерозигот, которая рассчитывается как 2рд. Итак, 2рд = 2 х 0,99 х 0,01 = 0,0198.
Это эквивалентно примерно 2% населения. Напомним, что это только приблизительный результат.
Следующая популяция находится в равновесии Харди-Вайнберга?
Если мы знаем число каждого генотипа в популяции, мы можем заключить, находится ли он в равновесии Харди-Вайнберга. Шаги для решения этого типа проблем следующие:
- Рассчитайте наблюдаемые генотипические частоты (D, H и R)
- Рассчитаем частоты аллелей (р и Q)
p = D + ½ H
q = R + ½ H
- Рассчитать ожидаемые генотипические частоты (р2, 2PQ и Q2)
- Рассчитать ожидаемые числа (р2, 2PQ и Q2), умножая эти значения на общее количество особей
- Сравните ожидаемые цифры с теми, которые наблюдались с помощью теста X2 от Пирсона.
Популяция бабочек
Например, мы хотим проверить, находится ли следующая популяция бабочек в равновесии Харди-Вайнберга: существует 79 особей гомозиготного доминантного генотипа (А.А.) 138 гетерозигот (Aa) и 61 рецессивный гомозигот (аа).
- Первым шагом является вычисление наблюдаемых частот. Мы делаем это путем деления числа особей по генотипу на общее число особей:
- D = 79/278 = 0,28
- H = 138/278 = 0,50
- R = 61/278 = 0,22
- Чтобы проверить, хорошо ли я сделал это первый шаг, я добавляю все частоты и должен дать 1.
Второй шаг – вычислить частоты аллелей..
- р = 0,28 + ½ (0,50) = 0,53
- Q = 0,22 + ½ (0,50) = 0,47
- С этими данными я могу рассчитать ожидаемые частоты генотипа (р2, 2PQ и Q2)
- р2 = 0,28
- 2pq = 0,50
- Q2 = 0,22
Я рассчитываю ожидаемые числа, умножая ожидаемые частоты на количество особей. В этом случае число наблюдаемых и ожидаемых особей одинаково, поэтому я могу сделать вывод, что население находится в равновесии.
Если полученные числа не совпадают, я должен применить вышеупомянутый статистический тест (X2 от Пирсона).
ссылки
- Andrews, C. (2010). Принцип Харди-Вайнберга. Знание о природе образования 3 (10): 65.
- Одесирк Т., Одесирк Г. и Байерс Б.Э. (2004). Биология: наука и природа. Пирсон Образование.
- Фриман, С. & Херрон, Дж. С. (2002). Эволюционный анализ. Прентис Холл.
- Футуйма, Д.Дж. (2005). эволюция . Sinauer.
- Hickman, C.P., Roberts, L.S., Larson, A., Ober, W.C., & Garrison, C. (2001). Интегрированные принципы зоологии (Том 15). Нью-Йорк: Макгроу-Хилл.
- Солер М. (2002). Эволюция: основа биологии. Южный Проект.
Генетика популяций. Микроэволюция. Закон Харди-Вайнберга
В процессе эволюции живых организмов ясно прослеживается тенденция к той или иной форме интеграции, которая проявляется, начиная с молекулярного уровня организации и заканчивается биосферным.
Интеграция позволяет осуществлять разделение функций между отдельными элементами системы, что делает саму систему более лабильной, жизнеспособной и экономичной.
Один из уровней интеграции, существующий между индивидуумом и видом, представлен популяцией.
Популяция — это группа особей одного вида, объединенных общим местом обитания. Она складывается под влиянием условий существования на основе взаимодействия трех факторов: наследственности, изменчивости и отбора. Особи внутри популяции обладают сходной системой приспособлений к условиям среды и из поколения в поколение воспроизводят основные адаптивные признаки.
Популяция является основной единицей эволюции. На эту роль популяция вышла благодаря следующим особенностям:
- Популяция — самовоспроизводящаяся система, способная к длительному существованию во времени и пространстве, в отличие от индивидуума, жизнь которого ограничена узкими временными рамками и который может не оставить потомства. В основе воспроизводства популяции лежит процесс размножения составляющих ее особей.
- Популяция является полномочным представителем вида, т.к. ее генофонд включает все основные гены видового уровня. В то же время в ней испытываются новые гены и их комбинации, за счет чего происходит обогащение видового генофонда.
- В популяции в результате скрещиваний осуществляется обмен генетической информацией между особями, который изменяет генотипическую структуру популяции, позволяя ей адекватно реагировать на разнообразные воздействия.
Основными характеристиками популяции являются: ее генофонд, численность, ареал и генотипическая структура. Все они динамичны, подвержены временным, иногда очень значительным, колебаниям. Динамические процессы, приводящие к изменению генетической структуры старых и формированию новых популяций, обозначают термином микроэволюция.
Исследования в области генетики популяций были начаты в первые годы ХХ в. Основателем этого направления считается датский генетик В. Иогансен, который разработал учение о популяциях и чистых линиях.
Изучая наследование количественных признаков в популяциях фасоли, Иогансен пришел к выводу о неэффективности отбора в чистых линиях и эффективности его в популяциях, в основе чего лежит генетическая однородность первых и гетерогенность вторых.
Открытие Иогансена, наряду с законами Менделя, способствовало созданию научных основ селекции.
Большинство популяций животных и растений складываются на основе свободного скрещивания особей — панмиксии. Это так называемые менделевские, или панмиктические, популяции раздельнополых животных и растений-перекрестников, в которых осуществляется постоянный обмен генетической информацией между ее членами.
Иной тип популяций образуют организмы, которым свойственно самооплодотворение или вегетативное размножение. В этом случае обмен генами между особями либо полностью исключен, либо затруднен.
Это так называемые закрытые популяции (растения-самоопылители, животные-гермафродиты), которые складываются как группы особей одного вида, имеющие общее происхождение, общий генофонд и общую систему адаптаций.
И, наконец, промежуточный тип характерен для популяций растений, в которых самоопыление чередуется с перекрестным, а половое размножение с апомиксисом (факультативные апомикты) или вегетативным размножением. Такие популяции обычно характеризуются сложной генетической структурой.
Особое положение в живой природе занимают популяции человека. Действие биологических факторов, изменяющих генетическую структуру популяции, в первую очередь естественного отбора, изменено в результате деятельности самого человека.
С помощью достижений науки, культуры, этики и медицины человек вносит существенные коррективы в процесс конструирования популяций, стремясь свести до минимума риск распространения “вредных” генов.
Однако существование человеческих популяций подчиняется тем же законам, которые действуют в других популяциях.
Основной закон генетики популяций был сформулирован в 1908 г. математиком Дж.Г. Харди в Англии и врачом В. Вайнбергом в Германии, независимо друг от друга, на основе данных, относящихся к популяциям человека.
Главный постулат этого закона сводится к тому, что частота гена не изменяется от поколения к поколению, а распределение генотипов в каждом поколении соответствует формуле бинома Ньютона, т.е.
определяется возведением в квадрат суммы частот двух аллелей.
Рассмотрим процедуру выведения этого закона. Возьмем достаточно большую по численности менделевскую популяцию, в которой присутствуют два аллеля одного гена: А и а.
В такой популяции будут встречаться три генотипа: АА, Аа и аа. Обозначим частоту доминантного аллеля через p, а рецессивного через q.
В случае свободного комбинирования гамет А и а частота каждого из трех генотипов будет равна: AA = p · p = p2; aa = q · q = q2.
Генотип Аа может возникнуть двумя путями: получив ген А — от матери, а ген а от отца, или же наоборот. Вероятность каждого из них равна pq, и, таким образом, общая частота генотипа Aa = pq + pq = 2pq.
- Геометрическое изображение закона Харди-Вайнберга можно представить в виде решетки Пеннета.
- F1
- p2 + 2pq + q2 = 1
- (p + q)2 = 1
Особи с генотипом АА будут образовывать один тип гамет с геном А с частотой p2. У особей с генотипом Аа будут формироваться два типа гамет: половина с А (pq) и половина с а (pq).
Особи с генотипом аа дадут все гаметы одного типа с геном а с частотой q2.
Общая частота гамет с геном А, таким образом, будет равна p2 + pq = p(p + q) = 1 = p, а гамет с геном а: q2 + pq = q(q + p) = q · 1 = q.
Следовательно, частота гамет, а значит и структура популяции (соотношение разных генотипов) в ней и в следующем поколении будут такими же. В этом случае говорят, что популяция находится в состоянии равновесия.
Закон Харди-Вайнберга имеет фундаментальное значение. Его формула позволяет рассчитывать частоту разных генотипов в популяции на основании фенотипического анализа.
Например, допустим, что в популяции коров животные с рецессивной красной мастью составляют 16%, остальные 84% имеют доминантную черную окраску. Следовательно, частота гомозиготного рецессива q2 = 0,16, а q, соответственно, равна 0,4. Так как p + q = 1, то p = 0,6.
Таким образом, частота гомозиготных черных животных p2 = 0,36, а гетерозиготных 2pq = 2 · 0,4 · 0,6 = 0,48.
Одно из интересных следствий, которое вытекает из закона Харди-Вайнберга, состоит в том, что редкие гены присутствуют в популяции в основном в гетерозиготном состоянии. Так, если частота рецессивного аллеля q = 0,01, то частота его у гомозигот q2 = 0,0001, а частота у гетерозигот pq = 0,01 · 0,99 ≈ 0,01, т.е. в гетерозиготном состоянии находится в 100 раз больше аллелей, чем в гомозиготном.
- Из этого следует вывод, что устранить вредную рецессивную мутацию из популяции практически невозможно: всегда будет существовать зона гетерозигот, где она будет прятаться под прикрытием доминантного гена.
- Формула Харди-Вайнберга применима для расчетов при следующих условиях:
- 1) если учитывается одна пара аллелей;
2) спаривание особей и сочетание гамет осуществляется случайно, т.е. нет ограничений на панмиксию;
- 3) мутации происходят настолько редко, что ими можно пренебречь;
- 4) популяция достаточно многочисленна;
- 5) особи с разными генотипами имеют одинаковую жизнеспособность.
Перечисленным условиям вряд ли может соответствовать хотя бы одна природная популяция. Закон справедлив для так называемой идеальной популяции. Но это ничуть не умаляет его значения.
В жизни каждой популяции существуют периоды, когда она находится в состоянии равновесия по частотам отдельных генов.
И если это равновесие по какой-либо причине нарушается, то популяция его достаточно быстро восстанавливает.
другие статьи темы 11 “Генетика и эволюция”:
► Вопросы и задания по теме “Генетика и эволюция”
Перейти к чтению других тем книги “Генетика и селекция. Теория. Задания. Ответы”:
Генетическая структура популяций. Закон Харди — Вайнберга
Одной из важных отраслей генетики является генетика популяций. Эта отрасль науки посвящена изучению генетической структуры природных популяций, а также генетических процессов, происходящих в ней. Она играет исключительно важную роль для развития эволюционной теории. Благодаря достижениям генетики популяций установлено, что популяция это не просто единица вида, но и единица эволюции.
Основоположником работ в этом направлении первой половине $XX$ века ($20$-е годы) стал С.С. Четвериков, русский генетик. Также, весомый вклад в развитие этой науки внесли:
- С.М. Гершинзон,
- Н.П. Дубинин,
- Д.Д.Ромашов,
- Р.Райт,
- Р.Фишер,
- Ф.Г.Добржанский.
Что же такое популяция? Современное определение этого понятия выглядит так:
Определение 1
«Популяция – это специфическая совокупность особей, принадлежащих одному виду, которой свойственно наличие общего генофонда и общая территория».
Закон Харди-Вайнберга
Так как популяция состоит из особей одного вида, то все они обладают одинаковым набором генов. Однако любой ген может быть представлен разными аллелями, количество которых может быть значительным.
Значит, популяция – это совокупность неодинаковых в генетическом отношении особей, которые отличаются разными состояниями свойственных им признаков.
В природе разные популяции одного и того же вида могут отличаться частотами встречаемости определенных аллельных генов.
Исследование закономерностей, которые распределяют аллели в популяциях, является важной задачей популяционной генетики. Над этой проблемой работали немецкий ученый В. Вайнберг и английский исследователь Г. Харди.
Они сделали вывод, что у достаточно многочисленной популяции, особи которой свободно скрещиваются между собой свободно, и без влияния какого-либо внешнего фактора на определенные сочетания аллелей, новые мутации не возникают , и обмен генетической информацией с другими популяциями в результате миграции особей в другие популяции не происходит, соотношение аллелей стабилизируется на протяжении нескольких поколений, затем на длительное время остается постоянным.
Закономерность, установленная Г. Харди и В. Вайнбергом, говорит о том, что при условии постоянства внешних и внутренних факторов частоты встречаемости аллелей у достаточно многочисленной популяции, которая изолированна от других, остается достаточно устойчивым на протяжении длительного периода.
Ученые предложили формулу, с помощью которой можно описать распределение частот в панмиксической популяции по одной паре аллельных генов ($A – a$). Эту формулу используют в качестве простейшей модели, служащей основой для проведения более сложных популяционно-генетических исследований.
$p^2AA + 2pqAa + q^2aa = 1$
Уравнение Харди-Вайнберга
${(q+p)}^2= q^2 + 2pq +p^2$, где:
- $q$ – частота встречаемости рецессивного гена;
- $p$ – частота встречаемости доминантного гена;
- $q^2$ – частоста встречаемости генотипа $aa$;
- $p^2$ – частоста встречаемости генотипа $AA$;
- $2pq$ – частота встречаемости генотипа $Aa$.
Исследования показали, что только при отсутствии свободного скрещивания, можно существенно повлиять на распределение частот встречаемости генотипов потомков.
Кроме того на изменения частот могут повлиять интенсивные миграции особей из между популяциями. Это приводит к активному обмену разными аллелями.
Мутации, происходящие в популяциях, также дают отклонение в показателях частот встречаемости аллелей.
Дрейф генов
Среди главных причин изменений генетической структуры популяций можно выделить дрейф генов.
Определение 2
Дрейф генов – это случайное ненаправленное изменение частоты встречаемости в популяциях аллелей.
Очень четко это явление проявляется в популяциях с немногочисленными особями, благодаря существующему ограничению свободного спаривания во время размножения. Но чем больше численность популяции, тем меньшее влияние на изменение частот встречаемости аллелей имеет дрейф генов.
Генетическая структура популяций
Популяции между собой отличаются частотой различных сочетаний аллельных генов.
Определение 3
Совокупность всех генов и их аллелей особей определенной популяции именуется генофондом.
Особое значение в генетике имеют рецессивные мутации. Рецессивные признаки распространяются в популяции в гетерозиготном состоянии, в фенотипе не проявляются.
Но со временем увеличивается вероятность образования гомозигот по рецессивному признаку. Тогда эти признаки проявляются в фенотипе. Если признак окажется полезным или нейтральным, он сохранится, если вредным – его носители просто погибнут.
Поэтому рецессивные мутации называют резервом наследственной изменчивости популяций.
Дрейф генов на ЕГЭ по биологии?! Не может быть! 26-е задание
Вы хотите познавать биологию и профессионально, и с удовольствием? Тогда вам сюда! Автор методики системно-аналитического изучения биологии и химии кбн Богунова В.Г. раскрывает тайны организации и функционирования живого, делится секретами мастерства при подготовке к любой форме экзамена (ОГЭ, ЕГЭ, ДВИ, олимпиада)
Мне всегда было интересно, школьные преподаватели биологии как-то проходят курсы повышения квалификации или продолжают забивать детям головы всем тем, что они с огромным трудом выучили на память в институте на заре эпохи динозавров? Почему я так возмущаюсь? Попробуйте задать вопросы ученику 10-11 класса и его учителю:
1) Что такое дрейф генов?2) О чем говорит закон Харди-Вайнберга?3) Плазмиды – это где?4) Транспозоны – это как?5) Почему ретровирусы так называются?
Это, всего лишь, немногие вспомнившиеся вопросы, затрагивающие далеко не самые последние открытия в науке. Так, понятие “дрейф генов” (как один из факторов эволюции) ввел генетик С.Райт в …
1931 г., существование транспозонов (мобильных генетических элементов) доказала цитогенетик Б.Мак-Клинток в … 1948 г., за что в 1983 г. получила Нобелевскую премию по физиологии и медицине.
Коллеги, просматривайте хотя бы научно-популярные статьи и вводите прочитанное в учебный материал. Только не нужно говорить “сколько платят, так и учим”! Неужели, самим не интересно?!
Однако, вернемся к основной теме статьи – “Дрейф генов на ЕГЭ”. В разделе “Пояснение репетитора” я обязательно расскажу о теоретической сути вопроса, а пока представлю одно из заданий 26-й позиции ЕГЭ и ответ моего ученика (оценка за ответ – 3 балла из 3).
Задание 26 (по памяти абитуриента)
Объясните, что такое популяционные волны и дрейф генов. В каких популяциях дрейф генов наиболее действенен?
Пояснение репетитора (экспресс-конспект)
Биологическая эволюция – процесс развития живой природы, который включает:
1) изменение генетического состава популяций 2) формирование приспособлений (адаптаций) 3) образование новых видов, более приспособленных к условиям среды4) вымирание менее приспособленных видов5) изменение биогеоценозов и биосферы
Основные тематические понятия:
Популяция (совокупность особей одного вида) – элементарная единица эволюции. Все эволюционные процессы начинаются внутри популяции, затрагивают и изменяют ее генофонд под действием факторов эволюции.
- Микроэволюция – эволюционные процессы, протекающие в популяциях вида, приводящие к изменению генофондов популяций, иногда – к образованию новых видов.
- Генофонд популяции – совокупность генотипов (аллелей) всех особей популяции.
- Факторы эволюции – движущие силы (причины), которые затрагивают, изменяют и закрепляют изменения генофондов популяций:
1) Наследственная изменчивость (мутационная и комбинативная)2) Популяционные волны (волны жизни)3) Изоляция популяций4) Миграции (генный поток)5) Дрейф генов6) Борьба за существование7) Естественный отбор
Популяционные волны (волны жизни) – периодическое чередование подъемов и спадов численности популяций, один из элементарных факторов эволюции. Термин был введен в 1905 г. С.С. Четвериковым. Примеры: нашествия полевок, мышей, саранчи и др.
С возрастанием численности популяции увеличивается число различных аллелей.
После спада численности особей часть аллелей случайно исчезнет вместе с несущими их особями, а некоторые аллели, сохранившиеся в выживших особях, резко повысят свою концентрацию.
Таким образом, популяционные волны, изменяя численность особей в популяции, способствуют изменению частот аллелей и генотипов. На стадии спада численности особей волны жизни ставят под угрозу выживание малочисленных популяций.
Дрейф генов – случайное ненаправленное изменение частоты генов (аллелей) в популяции. Например, лесную поляну населяет группа растений дикой гвоздики. Небольшое количество особей популяции содержит особый вариант аллеля, затрагивающий окраску цветка. Во время урагана упало дерево и растения с уникальной окраской цветка погибли, т.е. особый вариант аллеля исчез из популяции.
В популяциях с высокой численностью особей дрейф генов практически не влияет на изменение частоты аллелей.
В малых популяциях дрейф генов приобретает решающее значение.Случается, что в малой популяции в результате гибели ряда особей утрачивается более адаптивный аллель (т.е. ген, определяющий адаптационно важный признак), а фиксируется и сохраняется менее адаптивный аллель.
Дрейф генов, происходящий на фоне резкого снижения численности особей в популяции, называется эффект бутылочного горлышка. В такие периоды дрейф генов становится решающим фактором эволюции.
Примеры эффекта бутылочного горлышка:
1) Популяция гепардов около 300 лет назад прошла через узкое горлышко численности и современные гепарды являются потомками всего семи особей. Эффект бутылочного горлышка сказался на жизнеспособности всего вида: у гепардов повышена чувствительность к болезням и резко снижена плодовитость.
2) Эффект бутылочного горлышка сыграл значительную роль в эволюции популяций человека. Определенные аллели утрачивались полностью в одних популяциях и фиксировались в других. Доказательством этому является распределение аллелей А и В по системе групп крови АВ0 в популяциях людей разных стран и континентов.
Вы хотите поступить в медицинский? Обязательно посетите мой сайт Репетитор по химии и биологии. Здесь вы найдете огромное количество задач, заданий, теоретического материала и познакомитесь с моими учениками, многие из которых уже давно закончили ВУЗы и, работая врачами, спасают наши с вами жизни.На странице ВК я анонсирую свои публикации, вебинары, уроки, рассказываю и показываю решение задач и заданий, выкладываю новинки теоретического материала, конспекты и лекции. Добавляйтесь ко мне в друзья, и вы всегда будете в курсе всех событий, связанных с подготовкой к ЕГЭ, ДВИ, олимпиадам!Полный каталог статей репетитора Богуновой В.Г. вы найдете на странице сайта Статьи репетитораПодписывайтесь на YouTube-канал Репетитор по химии и биологии. Здесь ежедневно появляются новые вебинары, видео-уроки, видео-консультации, видео-решения.Пишите мне в WhatsApp +7(903)186-74-55, я отвечу вам обязательно.Приходите ко мне на занятия, я помогу вам фундаментально изучить химию и биологию, научу решать любые задачи, даже самые сложные.
Репетитор по химии и биологии кбн В.Богунова